An Artificial Intelligence for the 2048 game
A discussion about possible algorithms which solve the 2048 game arose on StackOverflow.
The main discussed algorithms are:
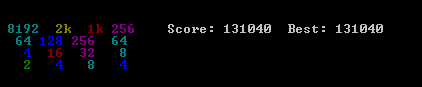
The solution I propose is very simple and easy to implement. Although, it has reached the score of 131040. Several benchmarks of the algorithm performances are presented.
This intuition will give you also the upper bound for a tile value: $2^{n} \rightarrow 2^{16} = 65536$ where $n$ is the number of tile on the board. (There's a possibility to reach the 131072 tile if the 4-tile is randomly generated instead of the 2-tile when needed)
Two possible ways of organizing the board are shown in the following images
To enforce the ordination of the tiles in a monotonic decreasing order, the score si computed as the sum of the linearized values on the board multiplied by the values of a geometric sequence with common ratio $r<1$ .
Several linear path could be evaluated at once, the final score will be the maximum score of any path.
An implementation of the minmax or the Expectiminimax will surely improve the algorithm. Obviously a more
sophisticated decision rule will slow down the algorithm and it will require some time to be implemented.I will try a minimax implementation in the near future. (stay tuned)
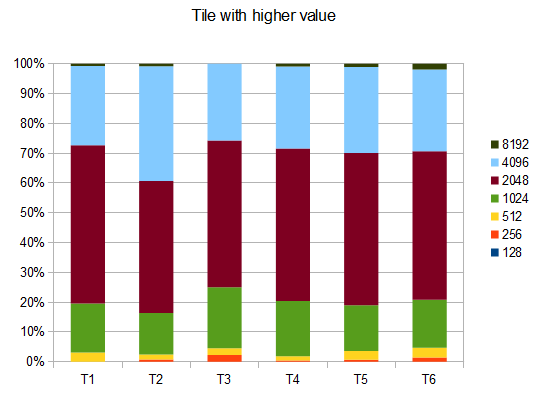
In case of T2, four tests in ten generate the 4096 tile with an average score of $\sim 42000$
- https://github.com/ov3y/2048-AI (ovolve)- A minimax approach which take into account several heuristic functions - I tested it out and it turned out to have some problems in reaching the 4098 tile in a reliable way
- https://github.com/nneonneo/2048-ai (nneonneo)- A very efficient implementation of an Expectiminimax approach with a quite simple heuristic - AFAIK he has reached the highest score of 173364 but I have not tried it yet
The solution I propose is very simple and easy to implement. Although, it has reached the score of 131040. Several benchmarks of the algorithm performances are presented.
Algorithm
Heuristic scoring algorithm
The assumption on which my algorithm is based is rather simple: if you want to achieve higher score, the board must be kept as tidy as possible. In particular, the optimal setup is given by a linear and monotonic decreasing order of the tile values.This intuition will give you also the upper bound for a tile value: $2^{n} \rightarrow 2^{16} = 65536$ where $n$ is the number of tile on the board. (There's a possibility to reach the 131072 tile if the 4-tile is randomly generated instead of the 2-tile when needed)
Two possible ways of organizing the board are shown in the following images
To enforce the ordination of the tiles in a monotonic decreasing order, the score si computed as the sum of the linearized values on the board multiplied by the values of a geometric sequence with common ratio $r<1$ .
$p_n \in Path_{0 \cdots N-1}$
$score = \sum_{n=0}^{N-1} value(p_n) * r^n$
Several linear path could be evaluated at once, the final score will be the maximum score of any path.
Decision rule
The decision rule implemented is not quite smart, the code in Python is presented here:An implementation of the minmax or the Expectiminimax will surely improve the algorithm. Obviously a more
sophisticated decision rule will slow down the algorithm and it will require some time to be implemented.I will try a minimax implementation in the near future. (stay tuned)
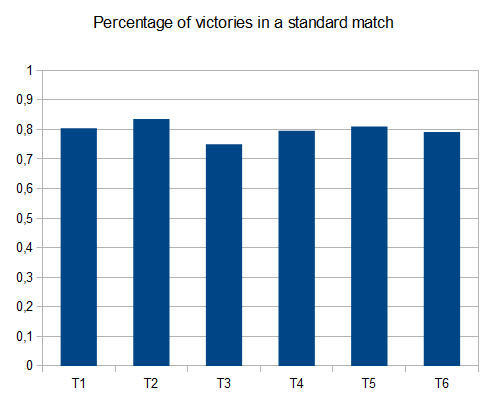
Benchmark
- T1 - 121 tests - 8 different paths - $r = 0.125$
- T2 - 122 tests - 8-different paths - $r = 0.25$
- T3 - 132 tests - 8-different paths - $r = 0.5$
- T4 - 211 tests - 2-different paths - $r = 0.125$
- T5 - 274 tests - 2-different paths - $r = 0.25$
- T6 - 211 tests - 2-different paths - $r = 0.5$
In case of T2, four tests in ten generate the 4096 tile with an average score of $\sim 42000$
Code
The code can be found on GiHub at the following link: https://github.com/Nicola17/term2048-AI
It is based on term2048 and it's written in Python. I will implement a more efficient version in C++ as soon as possible.
It is based on term2048 and it's written in Python. I will implement a more efficient version in C++ as soon as possible.
StackOverflow
You can upvote my answer on StackOverflow here :)